Data-Driven Mark Orientation for Trend Estimation in Scatterplots
(Proceedings of SIGCHI 2021)
Figure 1: The impact of mark orientation on trend estimation. When a trend in the data is unambiguous, either due to a strong correlation (a,b) or the presence of an obviously outlying cluster irrelevant to the central trend (c,d) mark orientation does not greatly impact the perception of trends in the data. However, when trends are ambiguous, mark orientation can introduce a bias. By using a data-driven orientation of marks in such cases, we can guide viewers to more accurate estimates of weak trends (e,f), or trends impacted by nearby outliers (g,h). This results in estimates that are robust even for cases when assumptions about an underlying linear modeling are violated.
Abstract:
A common task for scatterplots is communicating trends in bivariate data. However, the ability of people to visually estimate these trends is under-explored, especially when the data violate assumptions required for common statistical models, or visual trend estimates are in onflict with statistical ones. In such cases, designers may need to intervene and de-bias these estimations, or otherwise inform viewers about differences between statistical and visual trend estimations. We propose data-driven mark orientation as a solution in such cases, where the directionality of marks in the scatterplot guide participants when visual estimation is otherwise unclear or ambiguous. Through a set of laboratory studies, we investigate trend estimation across a variety of data distributions and mark directionalities, and find that data-driven mark orientation can help resolve ambiguities in visual trend estimates.Materials:
Paper: [PDF
3.6M] (CHI 2021).
Supp: OSF Link.
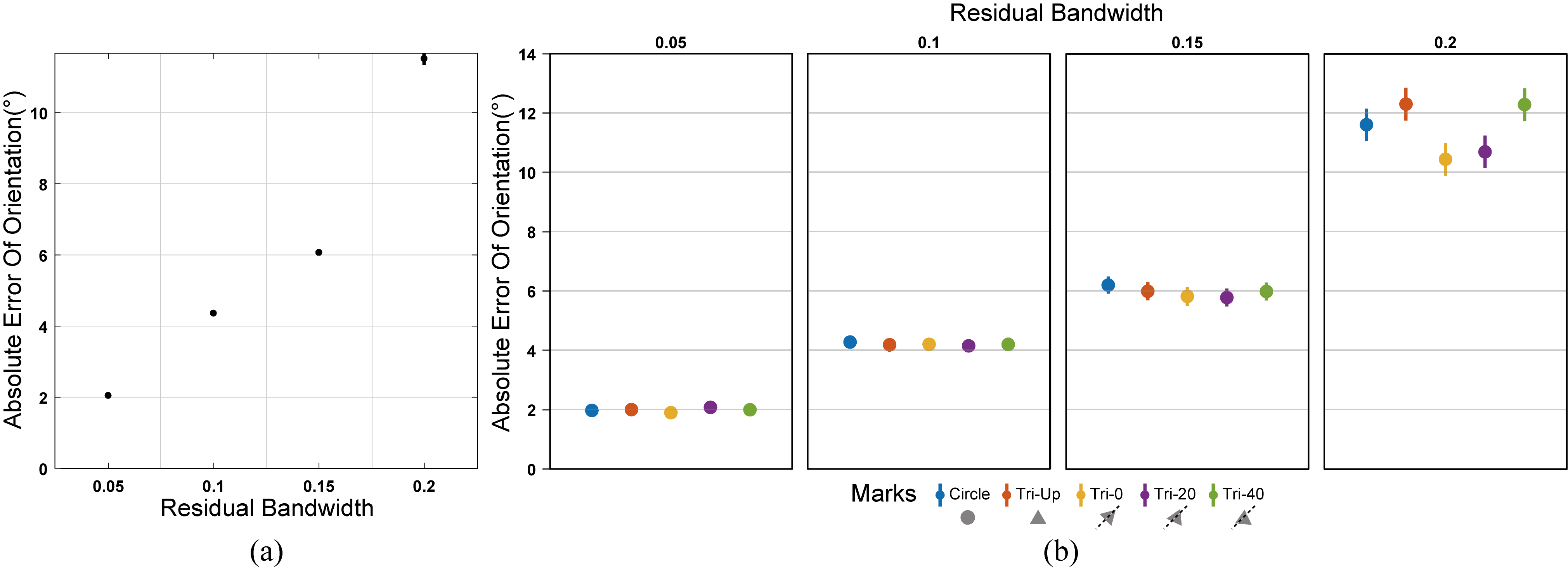
Figure 2: Results of Hypothesis 2 in Experiment 1: (a) Effect of residual bandwidth on accuracy of estimating trend orientation. The absolute orientation error increases monotonically as the bandwidth increases. (b) Effect of residual bandwidth and mark orientation on estimating trend orientation.

Figure 3: Scatterplots with four different marks explored in Experiment 2: (a) Circle; (b) Tri-Up; (c) Tri-R, and (d) Tri-O.
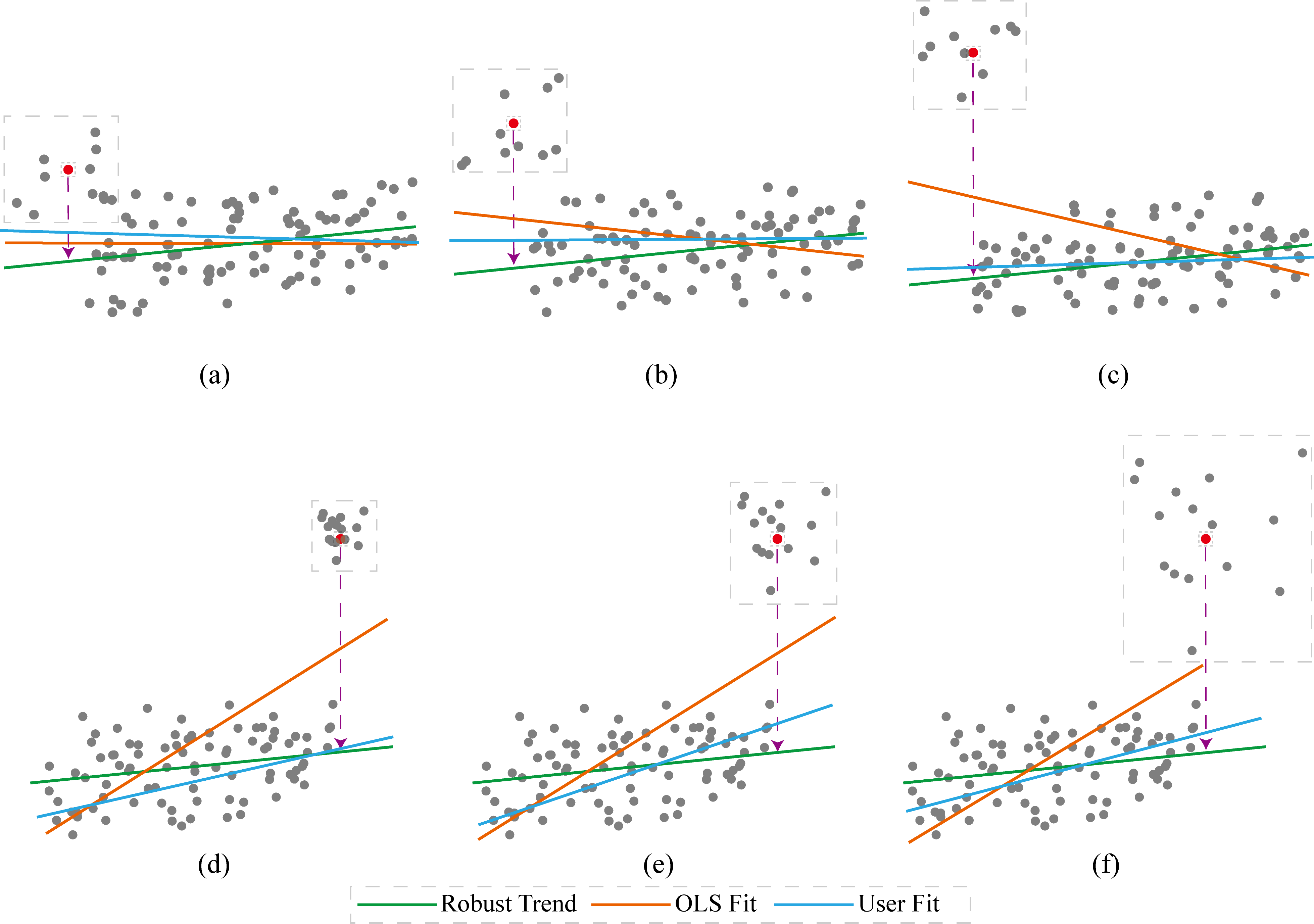
Figure 4: Three examples for outlier clusters with different distances (a,b,c) to the major cluster in y direction (distance indicated by the red dashed line) and three examples of outliers with different densities (d,e,f). The green line shows the robust trend line fitted only to the major cluster, while the orange line indicates the OLS trend line fitted to all points in both clusters.
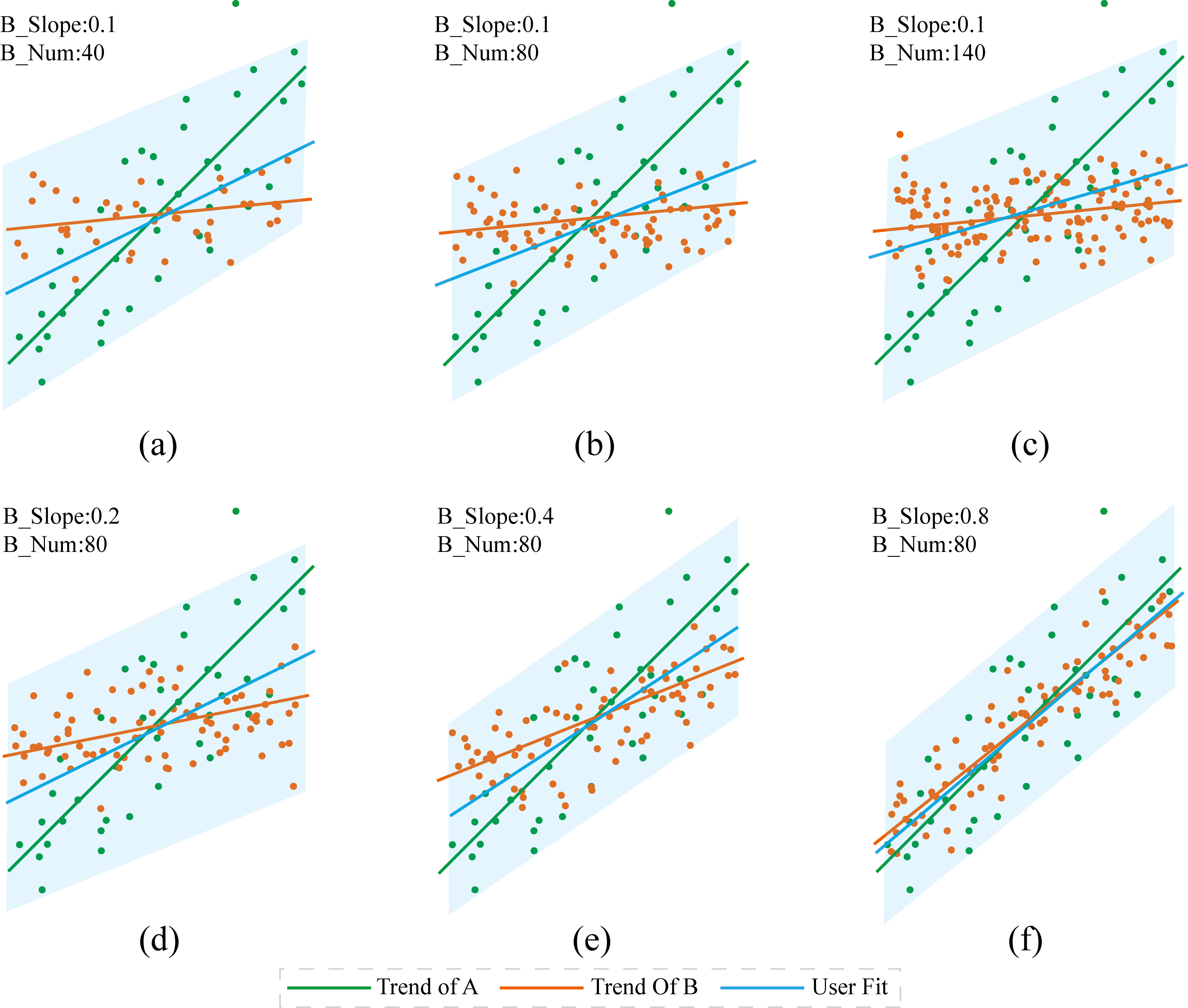
Figure 5: Scatterplots with varying point numbers and slope: (a,b,c) show varying point numbers in Set B; (d,e,f) show variations of the slope of Set B. The overlaid green line is the fitted trend line for point Set A, the orange line for point Set B; and the blue line is the user fit. The bounding box shown for each scatterplot is computed by discarding outliers.
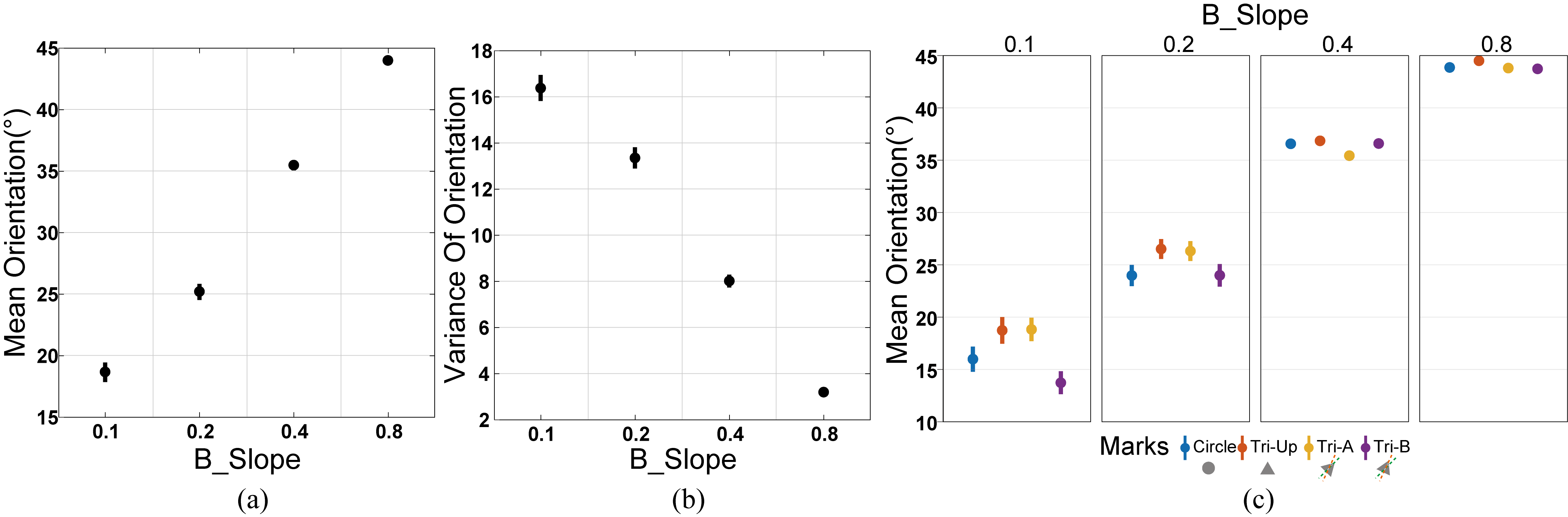
Figure 6: Results of Hypothesis 3 in Experiment 3: for our third experiment with intermixed point sets A and B, the effect of the slope of Set B on the estimation of trend orientation, in terms of both mean (a) and variance (b); (c) Effect of the interaction between the slope of Set B and mark orientation on trend estimation.

Figure 7: The scatterplots with different visual marks for studying the relation between sodium excretion and blood pressure. (a) The points with outliers shown in red and the OLS and robust trend lines; (b,c) two scatterplots with two different visual marks, Tri-O (b) and Tri-R(c).
Acknowledgement:
This work is supported by the grants of the NSFC (61772315, 61861136012), the Open Project Program of State Key Laboratory of Virtual Reality Technology and Systems, Beihang University (No.VRLAB2020C08), and the CAS grant (GJHZ1862).