Implicit Multidimensional Projection of Local Subspaces

(Proceedings of InfoVis 2020)

Rongzheng Bian¹ Yumeng Xue¹ Liang Zhou² Jian Zhang ³ Baoquan Chen ⁴ Daniel Weiskopf ⁵ Yunhai Wang ¹
¹Shandong University ²University of Utah ³CNIC,CAS ⁴Peking Univeristy ⁵University of Stuttgart

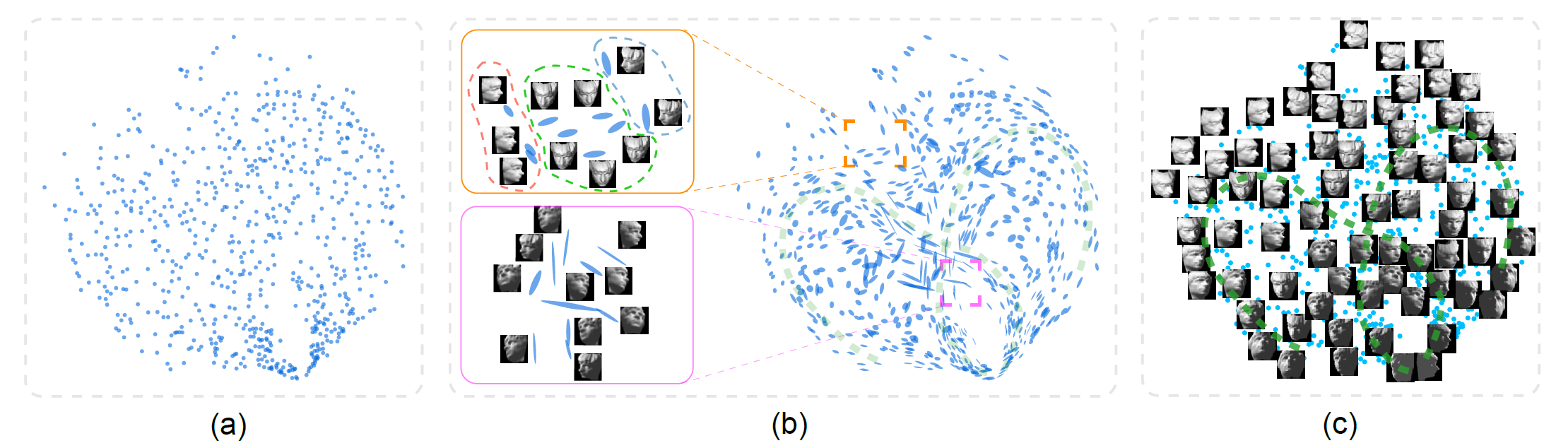
Figure 1: The face dataset is projected to 2D using nonlinear MDS. (a) Traditional visualization just shows the projected data points; here, no obvious correlation can be seen. (b) With our new implicit local subspace projection method, global trends and local structures (i.e., local linear subspaces around data points in the original high-dimensional space) are visualized through the orientation and shape of glyphs that replace the dots in the 2D plot. Now, two groups of glyphs associated with right- and left-facing faces are clearly separated (near the bottom), and some more of the interesting local patterns are identified in the zoom-ins. (c) Two trends that cross at the center of the plot are highlighted in green in the image view (also in (b), transparent dashed lines in green); such crossing would not be visible without the orientation encoding in our new glyphs.

Abstract:

We propose a visualization method to understand the effect of multidimensional projection on local subspaces, using implicit function differentiation. Here, we understand the local subspace as the multidimensional local neighborhood of data points. Existing methods focus on the projection of multidimensional data points, and the neighborhood information is ignored. Our method is able to analyze the shape and directional information of the local subspace to gain more insights into the global structure of the data through the perception of local structures. Local subspaces are fitted by multidimensional ellipses that are spanned by basis vectors. An accurate and efficient vector transformation method is proposed based on analytical differentiation of multidimensional projections formulated as implicit functions. The results are visualized as glyphs and analyzed using a full set of specifically-designed interactions supported in our efficient web-based visualization tool. The usefulness of our method is demonstrated using various multi- and high-dimensional benchmark datasets. Our implicit differentiation vector transformation is evaluated through numerical comparisons; the overall method is evaluated through exploration examples and use cases.

Materials:

Paper: [PDF 20.0M].
Supp: [PDF 60.8M].
Code: [GitHub].

Overview:

Figure 2: Workflow of our method: Dimensionalty reduction (left) projects points from the original space to the low-dimensional visualization space. We extend this conventional approach by first computing a linear subspace around each data point using local PCA and then projecting the basis vectors of the subspace to the low-dimensional visualization space. These transformed vectors are used to encode the deformation of the projected subspace in glyphs.

Results:

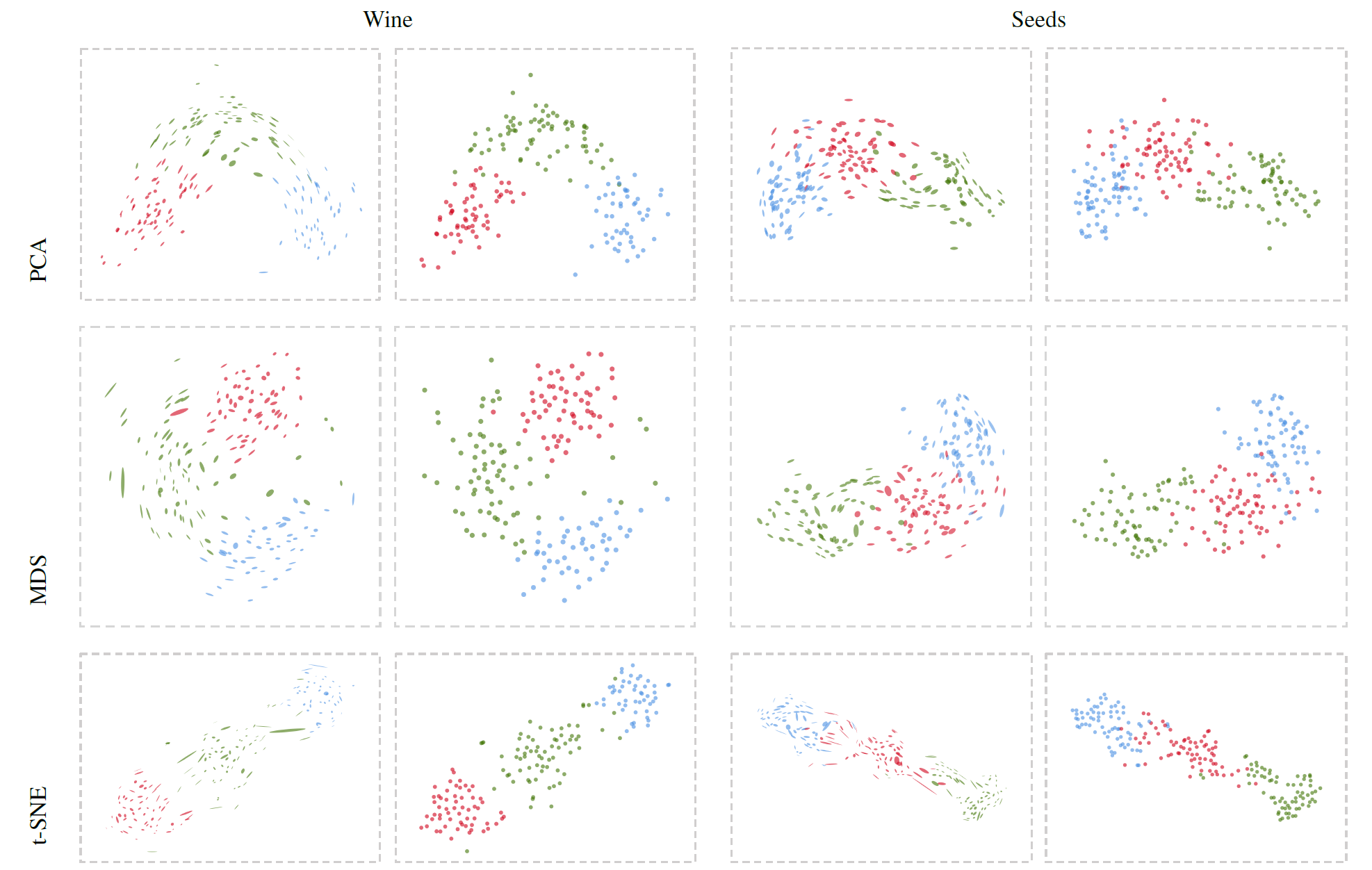
Figure 3: Visualizations of multidimensional datasets of Wine (first column) and Seeds (second column). Each projection method is visualized using our method (left boxes) and the point-based visualizations (right boxes). We can see global trends and twisting structures from the variations of local subspace glyphs.

Figure 4: Local subspace visualizations of the COIL dataset with PCA (first row), MDS (second row) shows that the different orientation and shape of the glyphs in adjacent areas correspond to different original data. And t-SNE (third row) shows that the orientation of glyphs changes smoothly within each cluster.

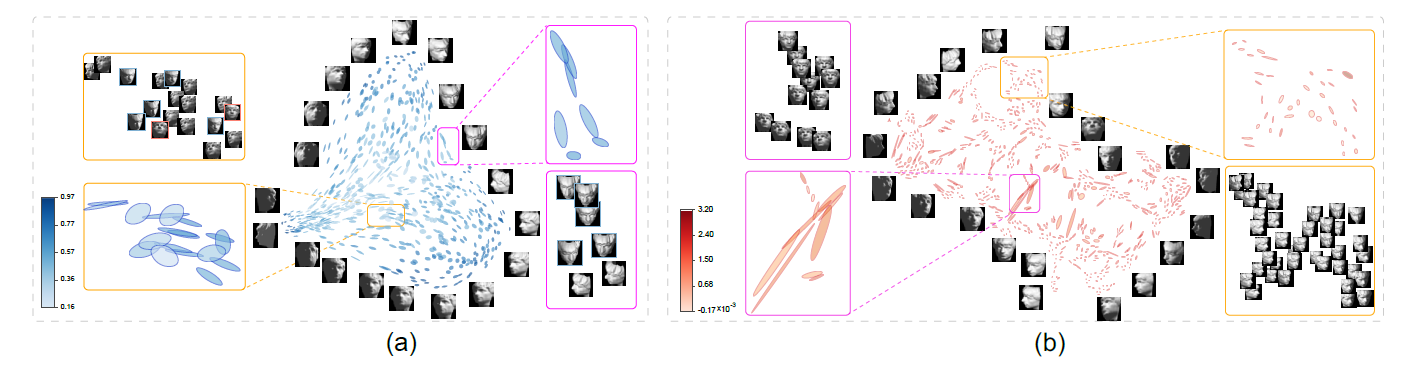
Figure 5: Local subspace visualizations of the Face dataset with PCA (a) and t-SNE (b), which are colorzed by two different quality metrics: trustworthiness and KL divergences, respectively. From the PCA result, we can see that two trends of glyphs separate around the center, one going upward and another going downward, and in each zoom-in, the distinct types of glyphs are associated with distinct face directions. From the t-SNE result, we can identify local patterns that exhibit trends.

Acknowledgements:

This work is supported by the grants of the National Key Research & Development Plan of China (2016YFB1001404), NSFC (61772315, 61861136012), by the Intel Graphics and Visualization Institutes of XeLLENCE, the National Institute of General Medical Sciences of the National Institutes of Health under grant numbers P41 GM103545 and R24 GM136986 and the Department of Energy under grant number DE-FE0031880 (USA), and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Project-ID 251654672 – TRR 161 (project B01).